Una particula P se mueve en una circunferencia. Colocamos un eje de coordenadas XY y en el origen O del sistema de coordenadas en el centro de la circunferencia.
Entonces es
Analogo a la velocidad y a la aceleracion podemos definir la velocidad angular ω así
y a la aceleracion angular α
Cuando t = 0 es también φ = 0, entonces es
![\varphi \left( t \right) = \int_0^t {\omega \,\operatorname{d} t} = \int_0^t {\left[ {\int_0^t {\alpha \,\operatorname{d} t} } \right]} \operatorname{d} t\,.](https://upload.wikimedia.org/math/2/7/5/2757758ecbebc67cf48d72a125ae8851.png)
- MCU(movimiento circular uniforme):
- Un movimiento circular con velocidad angular constante se lo llama uniforme. Entonces
La ecuacion del vector posición es
Con esto nos da la velocidad
y
Efectuando el producto escalar entre los vectores r y v obtenemos:
Con lo cual resulta que los vectores r y v son perpendiculares. Para la aceleracion tenemos que
y así
La aceleracion esta dirigida hacia O (aceleracion centripeta), y su modulo es constante. - MCUA(Movimiento circular uniformemente acelerado):
- Aqui la aceleracion angular α es constante y también ω(0) = 0También, cuando φ(0)=0, así para el angulo de rotacion
Asi tenemos también que
y
o
Asi, podemos dedecir que la componente radial de la aceleracion (y su direccion) es
y su componente tangencial es


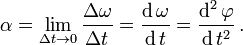
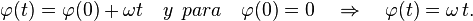
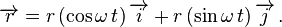


![\begin{align}
\overrightarrow r \, \cdot \overrightarrow v & = r\left( {\cos \omega \,t} \right) \left[- r\omega \left( {\sin \omega \,t} \right)\right] + r\left( {\sin \omega \,t} \right) r\omega \left( {\cos \omega \,t} \right) \\
& = - r^2 \omega \left( {\sin \omega \,t} \right)\left( {\cos \omega \,t} \right) + r^2 \omega \left( {\sin \omega \,t} \right)\left( {\cos \omega \,t} \right) \\
& = 0
\end{align}](https://upload.wikimedia.org/math/e/f/f/eff82b88dacb6d147a1289bf9db14f1d.png)


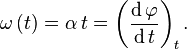
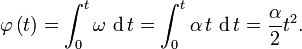

![\overrightarrow v = \frac{{\operatorname{d} \overrightarrow r }}
{{\operatorname{d} t}} = r\alpha \,t\left[ { - \left( {\sin \,\frac{\alpha }
{2}t^2 } \right)\overrightarrow i + \left( {\cos \frac{\alpha }
{2}t^2 } \right)\overrightarrow j } \right] = r\omega \left[ { - \left( {\sin \,\frac{\alpha }
{2}t^2 } \right)\overrightarrow i + \left( {\cos \frac{\alpha }
{2}t^2 } \right)\overrightarrow j } \right]](https://upload.wikimedia.org/math/5/2/6/526163d5925d1e0013eec1449ba3d8af.png)
![\overrightarrow a = \frac{{\operatorname{d} \overrightarrow v }}
{{\operatorname{d} t}} = r\alpha \left[ { - \left( {\sin \frac{\alpha }
{2}t^2 } \right)\overrightarrow i + \left( {\cos \frac{\alpha }
{2}t^2 } \right)\overrightarrow j } \right] +](https://upload.wikimedia.org/math/f/2/b/f2b7abd36b7ab46a91072ea3380cba89.png)
![+ \,r\alpha ^2 t^2 \left[ {\left( { - \cos \frac{\alpha }
{2}t^2 } \right)\overrightarrow i - \left( {\sin \frac{\alpha }
{2}t^2 } \right)\overrightarrow j } \right].](https://upload.wikimedia.org/math/6/f/2/6f22ae3c30a183200b9931ef6f9853dc.png)
![\overrightarrow a = \left[ { - r\alpha \left( {\sin \varphi } \right) - r\omega ^2 \left( {\cos \varphi } \right)} \right]\overrightarrow i +](https://upload.wikimedia.org/math/9/1/2/91211942147a28de3d28e927d9ec6122.png)
![+ \left[ {r\alpha \left( {\cos \varphi } \right) - r\omega ^2 \left( {\sin \varphi } \right)} \right]\overrightarrow j .](https://upload.wikimedia.org/math/7/1/3/71347ae6734f4b755258039108b9ca70.png)


No hay comentarios.:
Publicar un comentario